«Structural inhomogeneities in bulk metallic glasses»

Bulk metallic glasses are a new and fascinating materials class with advanced properties interesting from both scientific and technological point of view. They show, for instance, extremely high strength (stronger than steel) but suffer from brittleness at ambient temperature (like window glass). Their atomic structure is often more definable in terms of what it is not, than what it is. Consequently, the structure-property relationship is not well understood.

If you throw equal-sized balls in a bucket, the balls will be arranged randomly with more or less empty space between them. Nevertheless, some special nearest neighbour arrangements (i.e. short-range order) will be present as it is shown in the two-dimensional representation of small balls on a sheet (a).

Order in disorder

Order in disorder

The depicted atomic structures are referred to as amorphous. In a metallic glass the atoms composing the material are disorderly arranged similar to balls in a bucket with some short-range order.

(a) The hexagon represents one densely packed 2-dimensional motif containing a central ball surrounded by 6 balls. In a metallic glass the atoms composing the material are disorderly arranged similar to balls in a bucket with some short-range order. The corresponding atomic structure is referred to as amorphous.

In (b), an example of a 3-dimensional atomic packing of a simulated CuZr [Copper-zirconium] amorphous alloywith Cu atoms yellow and Zratoms red is shown. If atomic order is extended over larger distances than of nearest neighbours we call it medium-range order. One goal of the project is finding local atomic order in a disordered material.

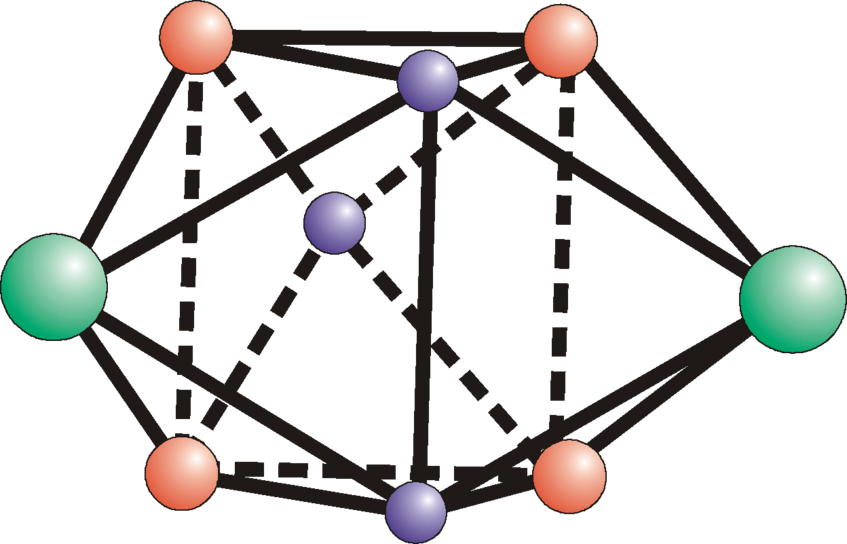
There are two types of ordering in glasses: Local order means atomic ordering in the R-range of first coordination spheres (less than ~5 Å). Local ordering includes topological ordering (geometry of “clusters”)...

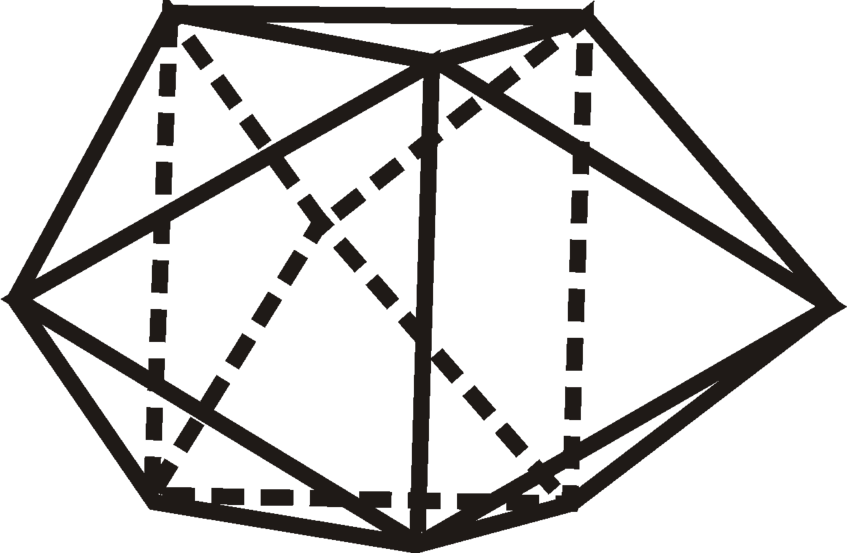
...and chemical ordering (order in arrangement of chemically different atoms).

Nanodiff

The movie shows localdiffraction images at different sample positions. The occurrence of speckles with high intensity in the diffraction patternindicates the presence of specialatomic clusters. The variation of the intensity between successive images is caused by the change of the local atomic structurewhen the beam is placed to a new sample position.

Medium range ordering means mutual arrangement of “clusters” as a whole in 3D-space (R-rang is ~10-15 Å).

To find atomic order in a disordered material we perform diffraction experiments with electronsaccelerated in a transmission electron microscope (TEM). Due to the wave nature of electrons (wave-particle duality) their interaction with atoms of the sample leads to interference phenomenaand observation of diffraction patterns.

In the case of small scattering volumes (containing a few atomic clusters only) by using smallelectron probes, local order information can be obtained. Statistical analyses of the intensity variations in a large set of diffraction patterns are used to extract atomic medium-range order out of the diffraction data. A measure of medium range order is the variance of the intensity.

Variance plot

The plot shows the normalizedvariance as a function of thescattering vector k for a CuZr(Copper-zirconium alloy) base bulk metallic glass. At certain k-values maxima (highest values of a function) occur. This indicates the presence ofatomic clusters of special configurations. The atomic structure of the clusters can be estimated by comparing the variance curve with peak positions of known crystalline structures (2 varieties ofMartensite and a B2 structure* in the plot above), as indicated by the vertical lines.

The plot shows the normalized variance as a function of the scattering vector k for a CuZr (Copper-zirconium alloy) base bulk metallic glass. At certain k-values maxima (highest values of a function) occur. This indicates the presence of atomic clusters of special configurations. The atomic structure of the clusters can be estimated by comparing the variance curve with peak positions of known crystalline structures (2 varieties of Martensite and a B2 structure* in the plot above), as indicated by the vertical lines. [→ read more ]

Local order of atoms in metallic glasses and the amount of empty space between the atoms (free volume) are considered as important parameters for the properties of bulk metallic glasses. To introduce more free volume or more medium-range order in the amorphous material we use externally driven processes of deformation and annealing. Referring to the model of balls in the bucket, annealing can be considered as shaking of the bucket to allow the balls to move and getting locally a denser (ordered) arrangement. The change of the atomic structure is traced by measuring the mechanical properties on a local micrometre scale.

Local hardness

The image shows the variation of local hardnessof a CuZr based bulk metallic glass afterstructural rejuvenation*. Each spot represents the hardness value of a region of a few micrometres. Spots of blue colour correspond to regions of strongly reduced hardness whereas spots of red colour are the hardest regions. The measurement reveals a strong heterogeneity of the amorphous structure as a consequence of the inhomogeneous rejuvenation process.

The image shows the variation of local hardness of a CuZr based bulk metallic glass after structural rejuvenation*. Each spot represents the hardness value of a region of a few micrometres. Spots of blue colour correspond to regions of strongly reduced hardness whereas spots of red colour are the hardest regions. The measurement reveals a strong heterogeneity of the amorphous structure as a consequence of the inhomogeneous rejuvenation process.

Research team

Principal Investigator: Prof. Christian Rentenberger

C. Ebner
S. Noisternig

Source Material - Attribution

[ more →] A detailed description of the results is published in C. Gammer et al., Sci. Rep. (2017).