«The influence of the coordination of crosslinks on the mechanical properties of polymers»
–Mussel threads and spaghetti in the computer
One can think of polymers as being long chain-molecules-a bit like spaghetti. In our case the spaghetti are even cooked, because the polymers are very flexible. Similar to a pile of spaghetti also a pile of polymers does not possess any mechanical stability, unless one ”glues” different parts of the spaghetti or polymers together. In this way one creates a continuous network out of the pile of independent threads. This network now possesses some mechanical stiffness and is not as easily deformable as the original threads. It is possible to use this process of cross-linking to specifically tailor the mechanical properties of the polymers.
Biological materials like bone, wood, silk or mussel-threads use cross-links that are relatively weak in strength, but are reversible. This means that a ruptured cross-link can re-form after the load is released. This mechanism provides some kind of self-healing. In a standard theoretical description a cross-link is described as an additional bond between two parts of one or two polymers. In the picture of the spaghetti this means that the cooked, sticky pasta are glued together at the positions where the pasta touches. Nevertheless, in nature a cross-link is often formed between more than only two partners. Using computer-simulations we aim at closing this gap in the theoretical description by explicitly investigating the influence of the number of contacts on the mechanical performance of cross-linked polymers
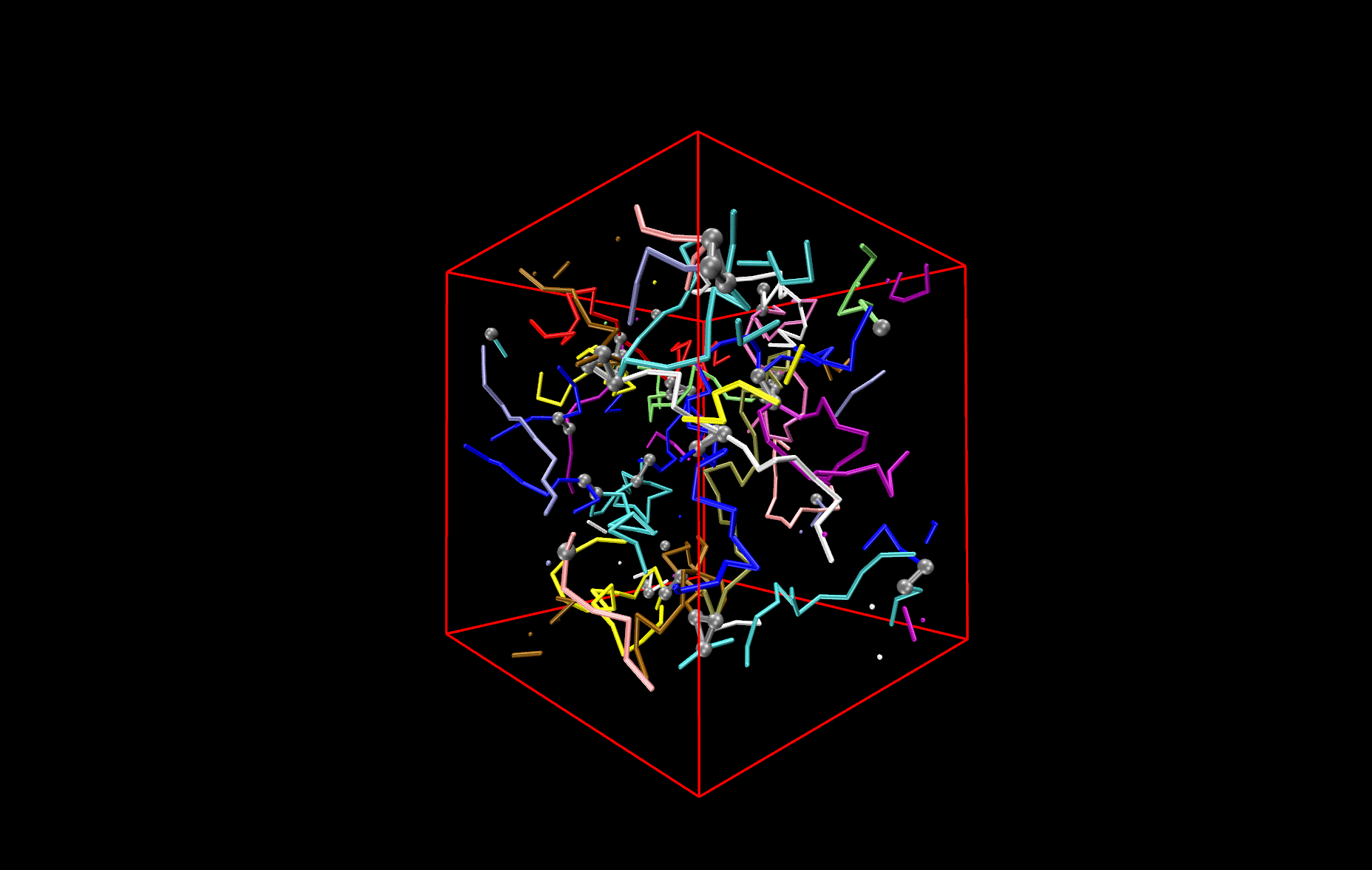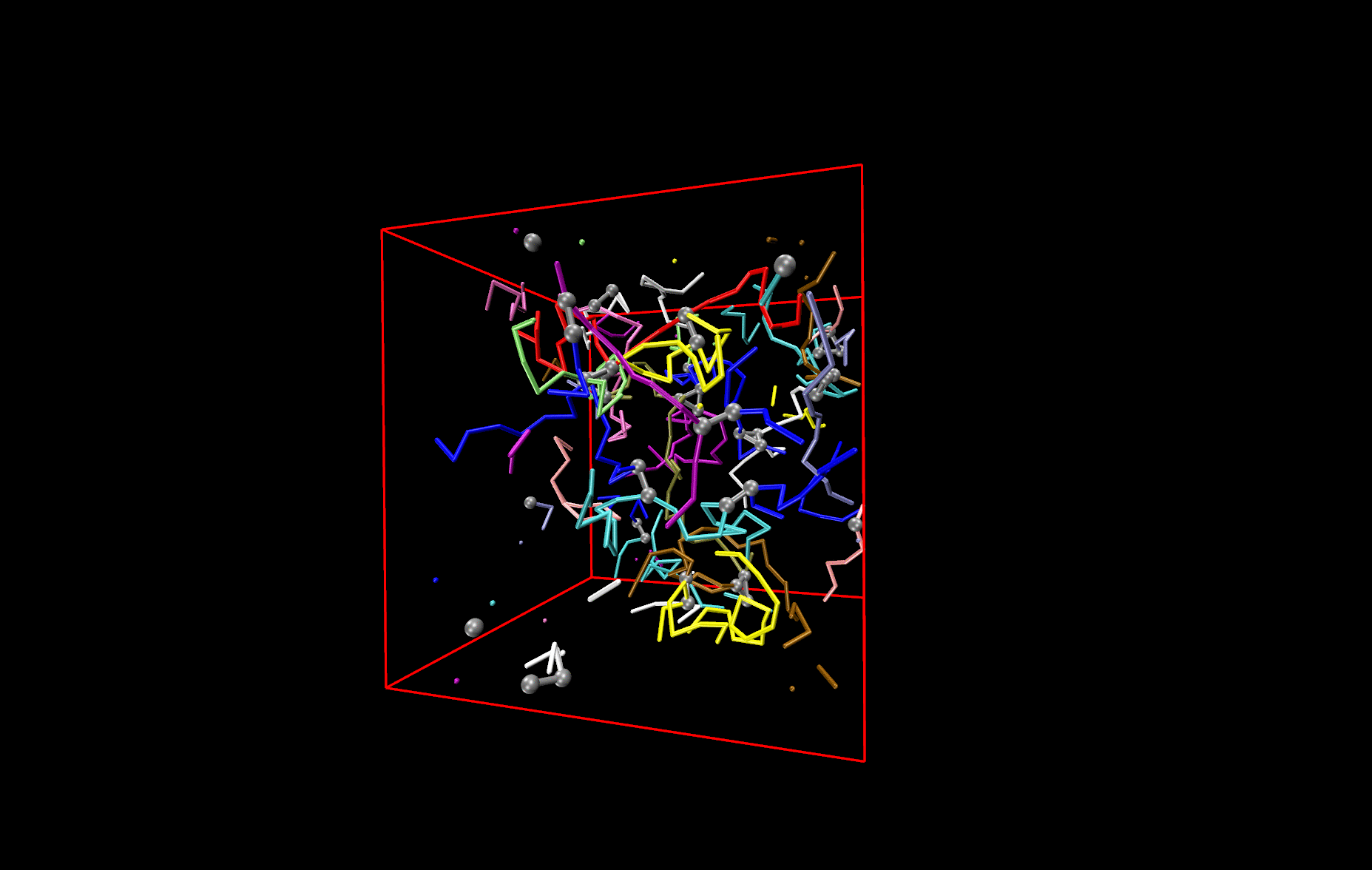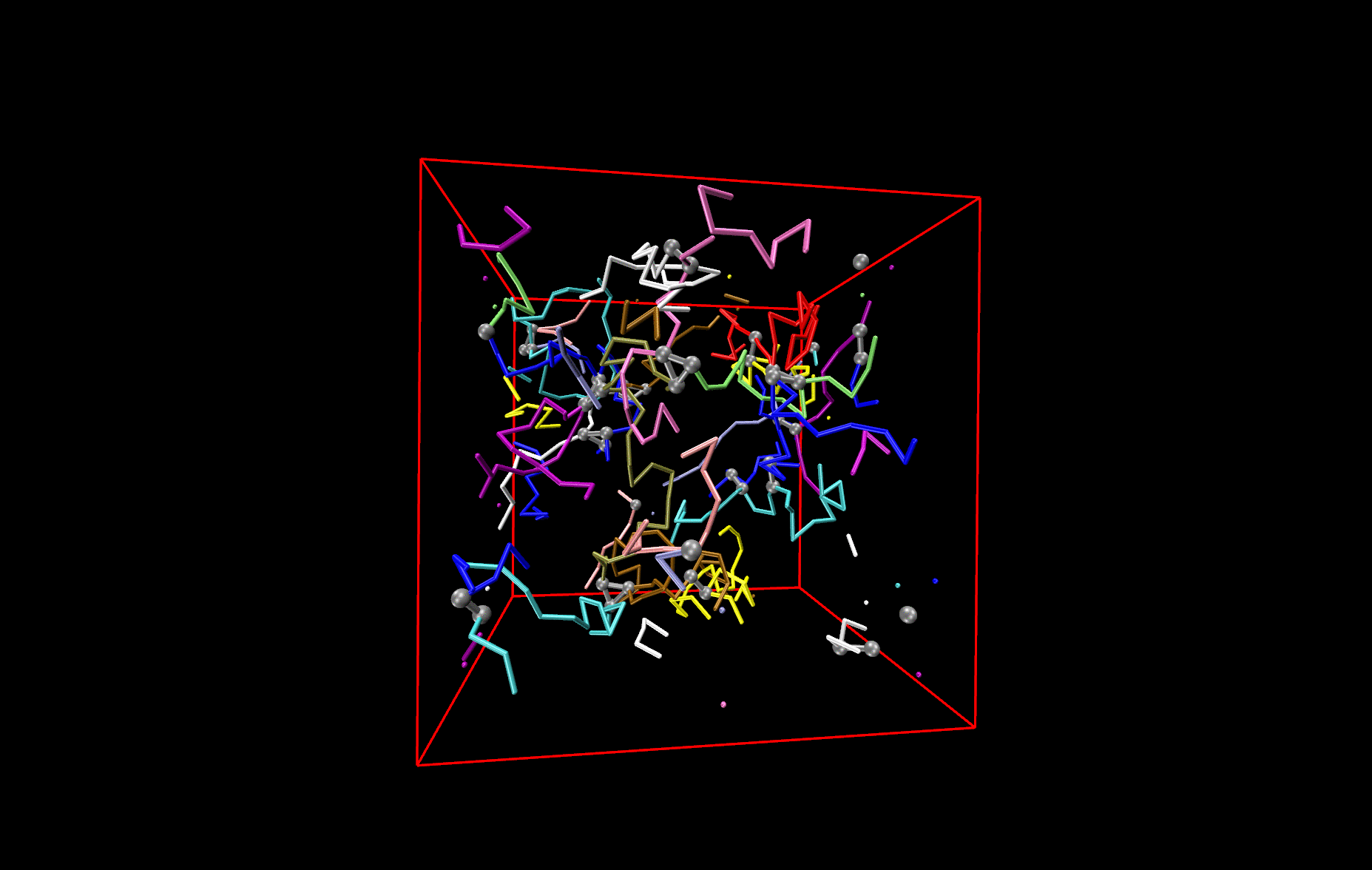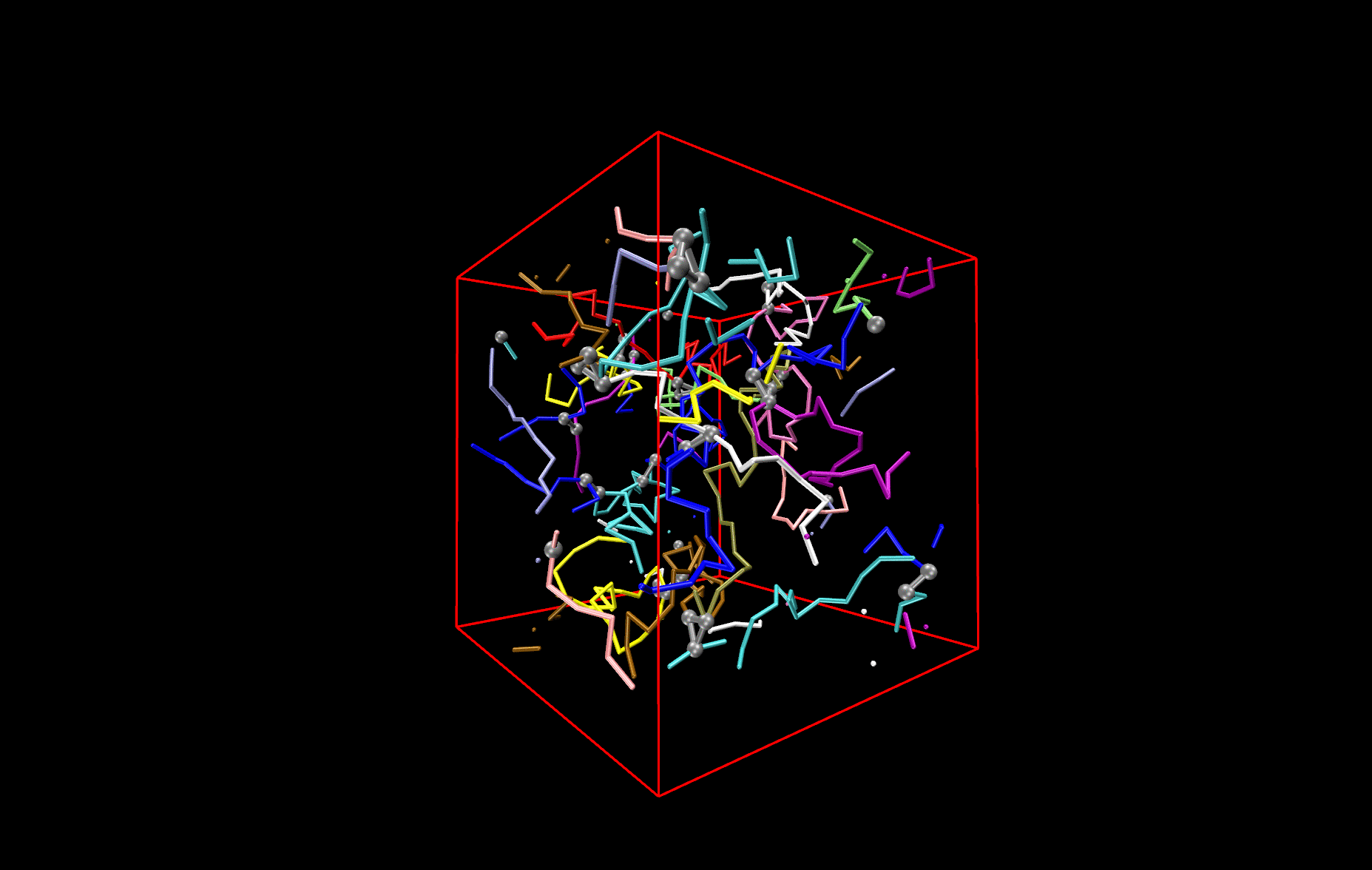
Polymer network
Polymer network
The picture shows a network made from differently colored polymers (spaghetti) that is held together by cross-links, made of three contacts. The cross-links are depicted by black balls and connecting bars. An important question to answer is how this network deforms, when one changes the size of the simulation box. Other questions that are investigated are how the deformation changes (i) if one changes the length of the spaghetti or (ii) if one switches from cooked to un-cooked spaghetti, i.e. if the polymers are not flexible like a thread, but stiff like un-cooked pasta.
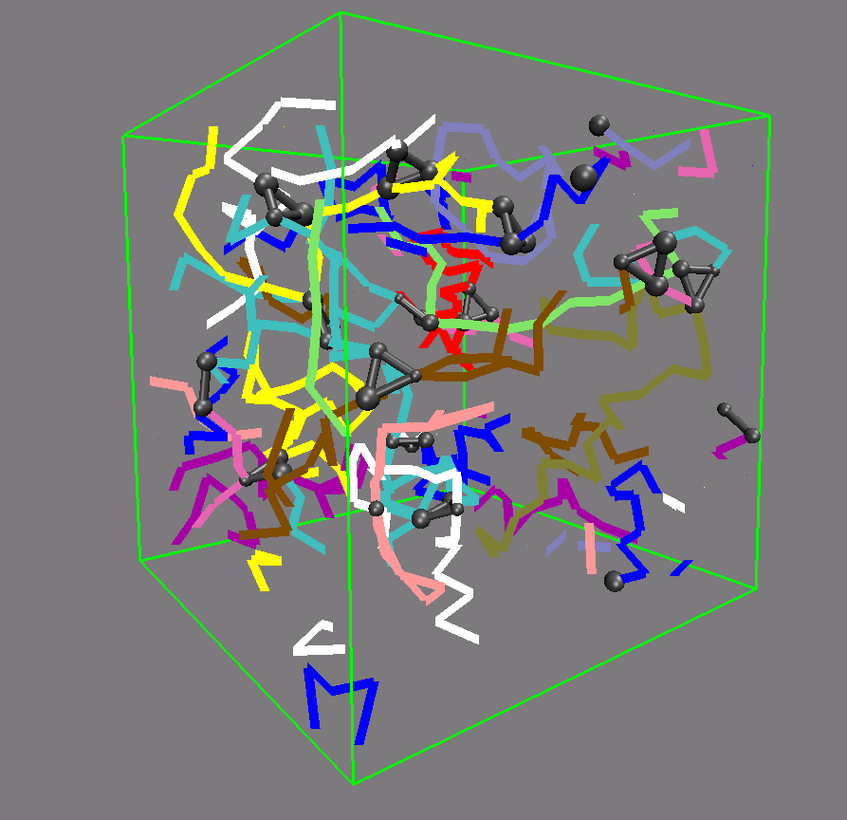
Network made of differently coloured polymers (Spaghetti).The cross-links are depicted by black balls and connecting bars.
The picture below shows a mussel that uses fine threads, i.e. its byssus, to adhere to a stone. These threads have to resist the high forces stemming from the waves and tides. The byssus threads are perfectly adapted to this task : they are relatively stiff, they can be extended up to the double of their original length without rupture, they possess a wear-resistant outer coating, they show self-healing and they naturally adhere under water. Responsible for these extraordinary properties are metal-coordination bonds that cross-link this material. These cross-links are most stable, when they form connections between three different parts of the polymers.

Mytilus with Byssus
Brocken Inaglory [Poly2]
The picture on the right shows the negative consequences of mussel adhesion. In the process of biofouling these materials adhere on wetted materials. Especially on ship hulls this is unwanted, because fouling significantly increases drag and, thus, increases fuel consumption. Due to the high adhesion strength of marine mussels cleaning is complex, time consuming and consequently expensive. A possible medical application is to implant a drug depot in arteries to treat arteriosclerosis. Currently, one main problem is to maintain the depot in place resisting the strong forces due to blood flow and a better understanding of the process is consequently of technological and medical importance.

Zebra Mussel [Poly3] : Negative consequences of mussel adhesion
The model
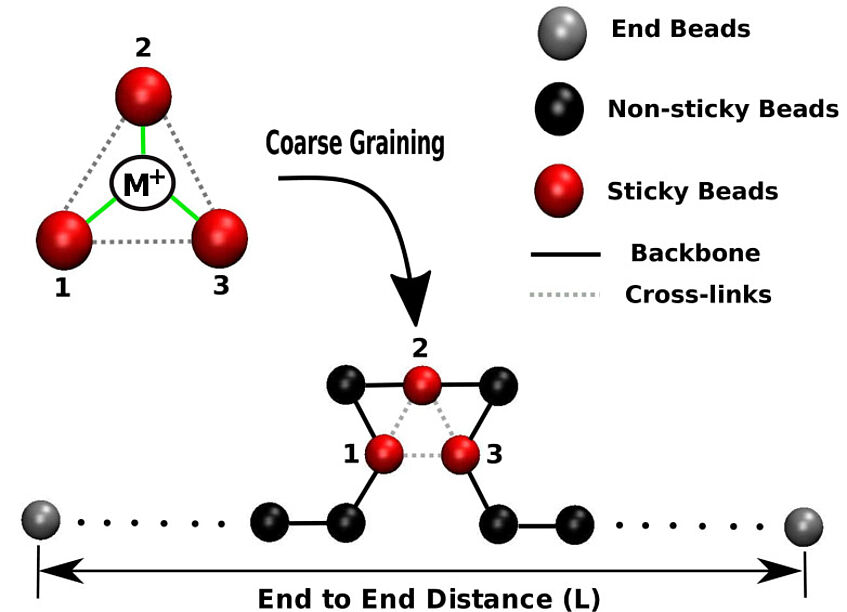
Schematic of cross-linking a single chain with a metal-ion
The picture shows a schematic of cross-linking a single chain with a metal-ion. The ion cross-linksthree parts of one or of different polymers. The number of cross-links changes the mechanical behavior of the chain. Where the number of cross-links is large, the deformation is small and where the number of cross-links is low, the deformation is high.
![[Poly5]](/fileadmin/_processed_/csm_07_Screenshot_ProgrammCode_b4befcf9eb.png)
The picture on the left shows a screenshot of the used computer code. The detail shows part of the sub-routine that is used to calculate the energetic contribution of the cross-links. The used methods are Monte-Carlo simulations. This method relies heavily on the use of random numbers, quite similar to playing roulette in the world-famous casino of Monte Carlo. This analogy gave the game its name.
Displacement
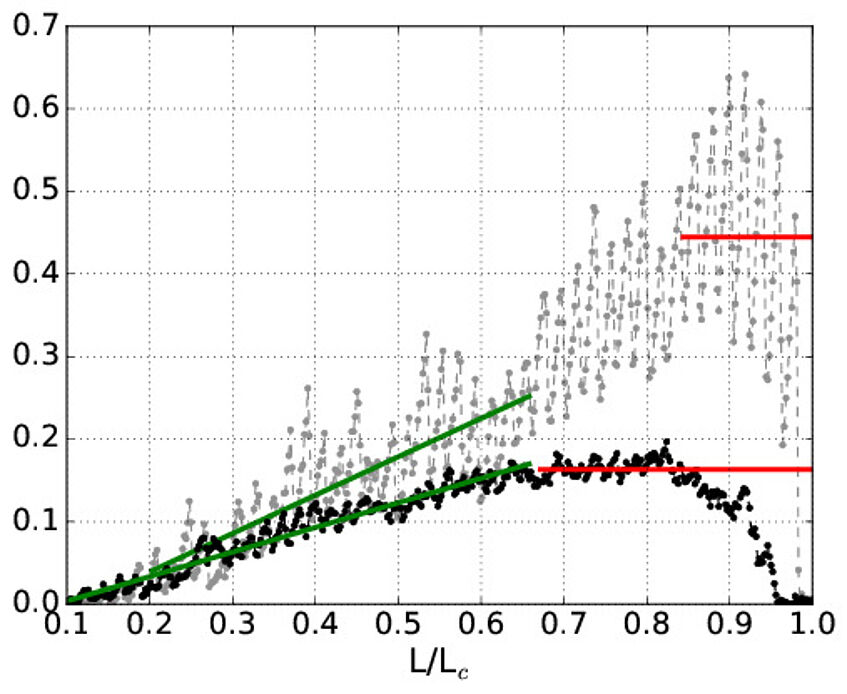
Displacement
Simulation of the force needed to pull different kinds of cross-links. The black symbols show a polymer where a cross-links connects three parts of a polymer, while the grey points correspond to cross-links that form solely between two partners.
The graph suggests a different mechanical behaviour: in the case of the three-fold coordinated structures (black) the curve is smoother, while the maximum force is smaller.
A typical result of a simulation. A cross-linked polymer is pulled in the computer and the force needed to do so is calculated. The figure shows two polymers that have the same number of cross-links, but where the cross-links are of different type. The black symbols show a polymer where a cross-links connects three parts of a polymer, while the grey points correspond to cross-links that form solely between two partners. The different mechanical behaviour is obvious. The curve is smoother for the three-fold coordinated structures, while the maximum force is smaller. This behavior will prove beneficial in network systems, because peak loads stemming from two-fold coordinated structures will be attenuated.
Trajectory
Deformation of a polymer with exactly one cross-link that connects three parts of the polymer.
The movie shows the deformation of a polymer with exactly one cross-link that connects three parts of the polymer. This cross-link consists of three bonds. During deformation first the two outermost parts of the polymer are stretched. Doing so the bond connecting the two most distant parts of the polymer fails. The two remaining bonds are not very stable and soon a single remaining bond between two parts of the polymers forms. It is this two-stage process of failing that makes a significant difference between three- and two-fold coordinated cross-links. For the latter, the rupture of one bond means the total loss of mechanical stability.
Research team
Principal Investigator: Dr. Markus A. Hartmann
- H. Shabbir